PRIMO COMPITO
Analisi due (Primo modulo) - Corso di Laurea in FISICA
Giovedì 7 Gennaio, 1999
  1. Si trovi la soluzione generale della seguente equazione:
    2. y¢¢-y¢-2y = 2e-x.
     
    SOLUZIONE: L'equazione omogenea associata y¢¢-y¢-2y = 0 ha polinomio caratteristico l2-l-2 = (l-2)(l+1). Quindi la soluzione del sistema omogeneo associato è yo(x) = c1e2x+c2e-x e il Wronskiano W(x) delle soluzioni è W = |
    e2x
     
    e-x
     
    2e2x
     
    -e-x
     
     | = -3ex Applichiamo il metodo della variazione dei coefficienti per determinare una soluzione particolare:
    yp(x) = - æ 
    ç 
    è     		 ó 
    õ     		 x 

    0 

    		 e-t·2e-t 
    W(t)    		 dt ö 
    ÷ 
    ø     		 e2x+ æ 
    ç 
    è     		 ó 
    õ     		 x 

    0 

    		 e2t·2e-t 
    W(t)    		 dt ö 
    ÷ 
    ø     		 e-x = 
     
     
    =  2 
    3    		 æ 
    è     		 ó 
    õ     		 x 

    0 

    		 e-3tdt ö 
    ø     		 e2x- 2 
    3    		 æ 
    è     		 ó 
    õ     		 x 

    0 

    		 dt ö 
    ø     		 e-x =  -2 
    9    		 e-x- 2 
    3    		 xe-x.
     
    Infine la soluzione generale è
    yo(x)+yp(x) = d1e2x+d2e-x- 2 
    3    		 xe-x.
     
  2. Si risolva il seguente problema di Cauchy:
    3. ì 
    ï 
    ï 
    í 
    ï 
    ï 
    î 
    y¢y¢¢ = 2 
     
    y(0) = 1
     
    y¢(0) = 2
     
     
     
    SOLUZIONE: Poniamo u = y¢. Tramite questa trasformazione l'equazione diventa
    ì 
    í 
    î 
    uu¢ = 2 
     
    u(0) = 2
     
     
     
    Che è un equazione a variabili separabili e ammette soluzione generale 1/2u2 = 2x+c. La condizione u(0) = 2 implica c = 2. Quindi risostituendo y¢ = u, si ha l'equazione
    ì 
    ï 
    ï 
    í 
    ï 
    ï 
    î 
    y¢(x) = 2   ___ 
    Öx+1 
     
     
    y(0) = 1
     
     
     
    Integrando otteniamo y(x) = 4/3(x+1)3/2+c e la condizione y(0) = 1 implica c = -1/3. Infine la solzione del problema di Cauchy è
    y =  4 
    3    		 (x+1)3/2- 1 
    3    		 .
     
  3. Si calcoli eA dove
    4. A =  æ 
    ç 
    è 
    -11 
     
    -3 
     
    36 
     
    10
     
         		 ö 
    ÷ 
    ø     		 .
     
    SOLUZIONE: Il polinomio caratteristico di A è
    l2+l-2 = (l-1)(l+2).
     
    Per ciascuno degli autovalori l1 = 1 e l2 = -2 gli autovettori v1 e v2 soddisfano (A-li)·vi = 0. Cioè
    æ 
    ç 
    è 
    -12 
     
    -3 
     
    36 
     
    9
     
         		 ö 
    ÷ 
    ø     		 v1 =  æ 
    ç 
    è     		 0 
    0    		 ö 
    ÷ 
    ø     		 ,  æ 
    ç 
    è 
    -9 
     
    -3 
     
    36 
     
    12
     
         		 ö 
    ÷ 
    ø     		 v2 =  æ 
    ç 
    è     		 0 
    0    		 ö 
    ÷ 
    ø     		 .
     
    Considerando solo le prime righe e facendo i calcoli possiamo scegliere:
    v1 =  æ 
    ç 
    è     		 1 
    -4    		 ö 
    ÷ 
    ø     		    e   v2 =  æ 
    ç 
    è     		 1 
    -3    		 ö 
    ÷ 
    ø     		 .
     
    Quindi se

    B = (
    1 
     
    1
     
    -4 
     
    -3
     
     ) con

    B-1 = (
    -3 
     
    -1
     
    4 
     
    1
     
     ), allora possiamo scrivere

    A = B(
    1 
     
    0 
     
    0 
     
    -2
     
     )B-1 e quindi

    eA = Be(
    1 
     
    0 
     
    0 
     
    -2
     
         		 )B-1 =  æ 
    ç 
    è 
    1 
     
    1
     
    -4 
     
    -3
     
         		 ö 
    ÷ 
    ø     		 æ 
    ç 
    è 
    e 
     
    0 
     
    0 
     
    e-2
     
         		 ö 
    ÷ 
    ø     		 æ 
    ç 
    è 
    -3 
     
    -1
     
    4 
     
    1
     
         		 ö 
    ÷ 
    ø     		 = 
     
     
    =  æ 
    ç 
    è 
    e 
     
    e-2
     
    -4e 
     
    -3e-2
     
         		 ö 
    ÷ 
    ø     		 æ 
    ç 
    è 
    -3 
     
    -1
     
    4 
     
    1
     
         		 ö 
    ÷ 
    ø     		 =  æ 
    ç 
    è 
    -3e+4e-2 
     
    -e+e-2
     
    12(e-e-2) 
     
    4e-3e-2
     
         		 ö 
    ÷ 
    ø 
     
  4. Sia
    5. A = {(x,y) Î R2 | x Î [-1,1) y Î (-1,1]} Ç {(x,y) Î R2 | x2+y2 ³ 1}.
     
    Dopo aver tracciato la figura di A, se ne determini l'interno, la chiusura, la frontiera e il derivato.

    SOLUZIONE: La figura di A è la seguente:

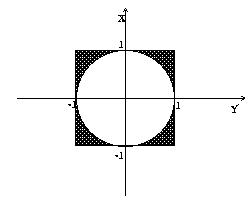
    L'interno: Ao = {(x,y)| x2+y2 > 1, x,y Î (-1,1)}.

    La chiusura: [`A] = {(x,y)| x2+y2 ³ 1, x,y Î [-1,1]}.

    La frontiera: A = {(x,y)| x2+y2 = 1}È({1,-1}×[-1,1])È([-1,1]×{1,-1}).

    Il derivato: D(A) = A.

  5. Si dimostri che il seguente sottoinsieme di R2 è denso in R2
    6. S = {(x,y) Î R2 t.c. y+x\not Î Z}.
     
    Si dimostri che il complementare di S non è discreto.

    SOLUZIONE: Per dimostrare la prima parte è equivalente fare vedere che ogni disco contiene elementi di S.

    Sia D un disco e sia p Î D un punto tale che p = (a,b) con a Î Q e b Î R\Q (tale p esiste per le proprietà dei numeri reali). È chiaro che a+b\not Î Z e quindi p Î S e DÇS ¹ Æ.

    Il complementare Sc di S contiene la retta x+y = 0. Sc non è discreto perchè (ad esempio) (0,0) è di accumulazione per Sc infatti per ogni e > 0, il punto (e/,-e/2) Î De((0,0))ÇSc. Quindi ogni intorno di (0,0) contiene punti di Sc\{(0,0)} e (0,0) non è isolato.

  6. Si discuta la continuità della seguente funzione f:R2®R su tutti i punti di R2:
    7. f(x,y) =  ì 
    ï 
    ï 
    ï 
    í 
    ï 
    ï 
    ï 
    î 
    x|y| 
    y2+|x|
     
    se  (x,y) ¹ (0,0)
     
     
    0
     
    se  (x,y) = (0,0)
     
     
     
    SOLUZIONE: Osserviamo che la funzione è sicuramente continua in tutti i punti (x,y) ¹ (0,0) in quanto espressione algebrica. Se (x,y) = (0,0), allora si noti che (utilizzando la diseguaglianza a/(a+b) £ 1 per a,b ³ 0)
    ê 
    ê 
    ê     		 x 
    y2+|x|    		 ê 
    ê 
    ê     		 £ 1.
     
    Quindi |f(x,y)| £ |y| e per il criterio del confronto, f è continua anche in (0,0).
  7. Si calcoli il differenziale nel punto (1,1) della funzione
    8. f(x,y) = sin p(x2+y2) 
    8    		 .
     
    Si trovi un punto (x0,y0) tale che df(x0,y0) = -[(p)/(Ö2)]dx?

    SOLUZIONE: Le derivate parziali sono:

    f 
    x    		 =  2xp 
    8    		 cos p(x2+y2) 
    8    		 ,  f 
    y    		 =  2yp 
    8    		 cos p(x2+y2) 
    8    		 .
     
    Quindi df(1,1) = [(pÖ2)/8](dx+dy).

    Per avere df(x0,y0) = -[(p)/(Ö2)]dx bisogna porre [(f)/(x)] = -[(p)/(Ö2)] e [(f)/(y)] = 0. La seconda condizione è soddisfatta ad esempio per y0 = 0 e con questa scelta la prima condizione diventa: [(x0p)/4]cos[(p(x02))/8] = -[(p)/(Ö2)]. Scegliendo x0 = Ö8, otteniamo un identità. Infine (x0,y0) = (Ö8,0).

  8. Si calcoli l'equazione della quadrica tangente nel punto (0,[(p)/2]) della funzione f(x,y) = xcos(y+x).

    9. SOLUZIONE: L'equazione della quadrica tangente in p = (0,[(p)/2]) è la seguente:

    Q(x,y) = f(p)+fx(p)x+fy(p)(y-p)+
     
     
    + 1 
    2    		 á (x,(y-p)), æ 
    ç 
    è 
    fxx(p) 
     
    fxy(p) 
     
    fxy(p) 
     
    fyy(p)
     
         		 ö 
    ÷ 
    ø     		 (x,(y-p)) ñ
     
    I calcoli delle derivate sono:
    fx = cos(y+x)-xsin(y+x),   fxx = -2sin(y+x)-xcos(y+x)
     
     
    fy = -xsin(y+x),   fyy = -xcos(x+y),
     
     
    fxy = -sin(y+x)-xcos(y+x).
     
    Sostituendo il punto p, otteninamo fx(p) = 0, fxx(p) = -2, fy(p) = 0, fyy(p) = 0, fxy(p) = -1 e quindi
    Q(x,y) = -2x2-x(y-p/2).
     
  9. Sia f(x,y) = arctan(y)·arctan(x-1). Determinare i punti critici di f e classificarli con il metodo della matrice Hessiania.

    10. SOLUZIONE: I punti critici soddisfano Ñ(f) = (0,0). Il gradiente è

    Ñ(f) =  æ 
    ç 
    è     		 (arctany) 
    1+(x-1)2    		 , arctan(x-1) 
    1+y2    		 ö 
    ÷ 
    ø     		 .
     
    Quindi l'unico punto critico (1,0). La matrice Hessiana è
    æ 
    ç 
    ç 
    ç 
    ç 
    ç 
    è 
    (arctany)2(1-x) 
    (1+(x-1)2)2
     
    1 
    (1+y2)(1+(x-1)2)
     
    1 
    (1+y2)(1+(x-1)2)
     
    -2yarctan(x-1) 
    (1+y2)2
     
         		 ö 
    ÷ 
    ÷ 
    ÷ 
    ÷ 
    ÷ 
    ø 
     
    Che nel punto (1,0) è

    (
    0 
     
    1 
     
    1 
     
    0
     
     ). Quindi, essendo l'Hessiana indefinita, il punto (1,0) è una sella.

  10. Siano
    11. f(x,y) = ln(x2+3+cos(y)),    g(t) = Öt,    h(t) = arccost
     
    e F(t) = f(g(t),h(t)). Utilizzare la regola di derivazione delle funzioni composte per calcolare
    d 
    dt    		 F(t).
     
    SOLUZIONE: La formula di derivazione delle funzioni composte afferma che
    d 
    dt    		 F(t) =  f 
    x    		 (g(t),h(t))g¢(t)+ f 
    x    		 (g(t),h(t))h¢(t) = 
     
     
    =  2Öt 
    3+2t    		 1 
    2Öt    		 + -sin(arccost) 
    3+2t    		 -1 
      ____ 
    Ö1-t2 
     
         		 =  2 
    3+2t    		 .
     
     
File translated from TEX by TTH, version 1.94.
On 7 Jan 1999, 15:26.