COMPITO DI METÀ SEMESTRE
Analisi due (Primo modulo) - Corso di Laurea in FISICA
Sabato 21 Novembre, 1998
  1. Si trovi la soluzione generale della seguente equazione:
    2. (a) y¢¢¢-5y¢¢+7y¢-3y = 0
     
     
    (b) y¢¢¢+5y¢¢+7y¢+3y = 0
     
    SOLUZIONE:(a) Il polinomio caratteristico dell'equazione l3-5l2+7l-3 si fattorizza in (l-3)(l-1)2. La soluzione associata alla radice l1 = 3 è e3x e le soluzioni associate alla radice doppia l2,3 = 1 sono ex e xex. La soluzione generale quindi è y(x) = c1e3x+(c2+c3x)ex.
    (b) Il polinomio caratteristico dell'equazione l3+5l2+7l+3 si fattorizza in (l+3)(l+1)2. La soluzione associata alla radice l1 = -3 è e-3x e le soluzioni associate alla radice doppia l2,3 = -1 sono e-x e xe-x. La soluzione generale quindi è y(x) = c1e-3x+(c2+c3x)e-x.
  2. Si risolva il seguente problema di Cauchy:
    3. (a) ì 
    ï 
    ï 
    í 
    ï 
    ï 
    î 
    y¢ =  y 
    x    		 + x 
    y
     
    y(1) = 1
     
     
     
     
    (b) ì 
    ï 
    ï 
    í 
    ï 
    ï 
    î 
    y¢ =  y 
    x    		 - x 
    y
     
    y(1) = 2
     
     
     
    SOLUZIONE:(a) Si tratta di un equazione omogenea. La trasformazione standard u = y/x (in modo che y¢ = u+xu¢) porta all'equazione a variabili separabili xu¢ = 1/u che ha soluzione generale (u(x))2 = c+2lnx e quindi (y(x))2 = cx2+2x2lnx. Osservando che 1 = y(1) > 0 si ottiene che 1 = y(1)2 = c+2ln1 e quindi la soluzione è y(x) = xÖ{1+2lnx}.
    (b) Si tratta di un equazione omogenea. La trasformazione standard u = y/x (in modo che y¢ = u+xu¢) porta all'equazione a variabili separabili xu¢ = -1/u che ha soluzione generale (u(x))2 = c-2lnx e quindi (y(x))2 = cx2-2x2lnx. Osservando che 2 = y(1) > 0 si ottiene che 4 = y(1)2 = c+2ln1 e quindi la soluzione è y(x) = xÖ{4-2lnx}.
  3. Si determini la soluzione generale del seguente sistema di equazioni differenziali e si classifichi il flusso associato allo spazio delle soluzioni:
    4. (a)  ì 
    í 
    î 
    y1¢ = y1+3y2
     
    y2¢ = -y1-y2
     
     
     
     
    (b)  ì 
    í 
    î 
    y1¢ = y1+2y2
     
    y2¢ = -y1-y2
     
     
     
    SOLUZIONE:(a) La matrice associata al sistema è ([1   3 || ( -1 -1)]) e ha polinomio caratteristico l2+2 = (l-Ö2i)(l+Ö2i). Gli autovettori (v1,v2) associati a Ö2i soddisfano (1-Ö2i)v1+3v2 = 0 e quindi possiamo prendere (v1,v2) = (3,Ö2i-1). Infine, una base per lo spazio delle soluzioni del sistema si ottiene considerando la parte reale e la parte immaginaria di ((3(cosÖ2x+isinÖ2x)) || ( (Ö2i-1)(cosÖ2x+isinÖ2x))) e quindi la soluzione generale è
    ì 
    í 
    î 
    y1(x) = 3c1cosÖ2x+3c2sinÖ2x
     
    y2(x) = -c1(cosÖ2x+Ö2sin2x)+c2(Ö2cosÖ2x-sinÖ2x)
     
         		 .
     
    Il flusso associato allo spazio delle soluzioni è un centro in quanto gli autovalori sono numeri complessi puramente immaginari.
    (b) La matrice associata al sistema è ([1   2 || ( -1 -1)]) e ha polinomio caratteristico l2+1 = (l-i)(l+i). Gli autovettori (v1,v2) associati a l = i soddisfano (1-i)v1+2v2 = 0 e quindi possiamo prendere (v1,v2) = (2,i-1). Infine, una base per lo spazio delle soluzioni del sistema si ottiene considerando la parte reale e la parte immaginaria di ((2(cosx+isinx)) || ( (i-1)(cosx+isinx))) e quindi la soluzione generale è
    ì 
    í 
    î 
    y1(x) = 2c1cosx+2c2sinx
     
    y2(x) = -c1(cosx+sinx)+c2(cosx-sinx)
     
         		 .
     
    Il flusso associato allo spazio delle soluzioni è un centro in quanto gli autovalori sono numeri complessi puramente immaginari.
  4. Sia Dom(f) il dominio della funzione
    5. (a) f(x,y) =    æ 
    Ö
    e-xy(y+2+x2) 
     
     
     
    (b) f(x,y) =    æ 
    Ö
    exy(y+2-x2) 
     
     
    Dopo aver tracciato la figura di Dom(f), se ne determini l'interno, la chiusura, la frontiera e il derivato.
    SOLUZIONE:(a) Il dominio della funzione si ottiene risolvendo la disequazione y+2+x2 ³ 0 (l'esponenziale, in quanto sempre positivo è ininfluente ai fini dell'esistenza della funzione). Il grafico:
     
     

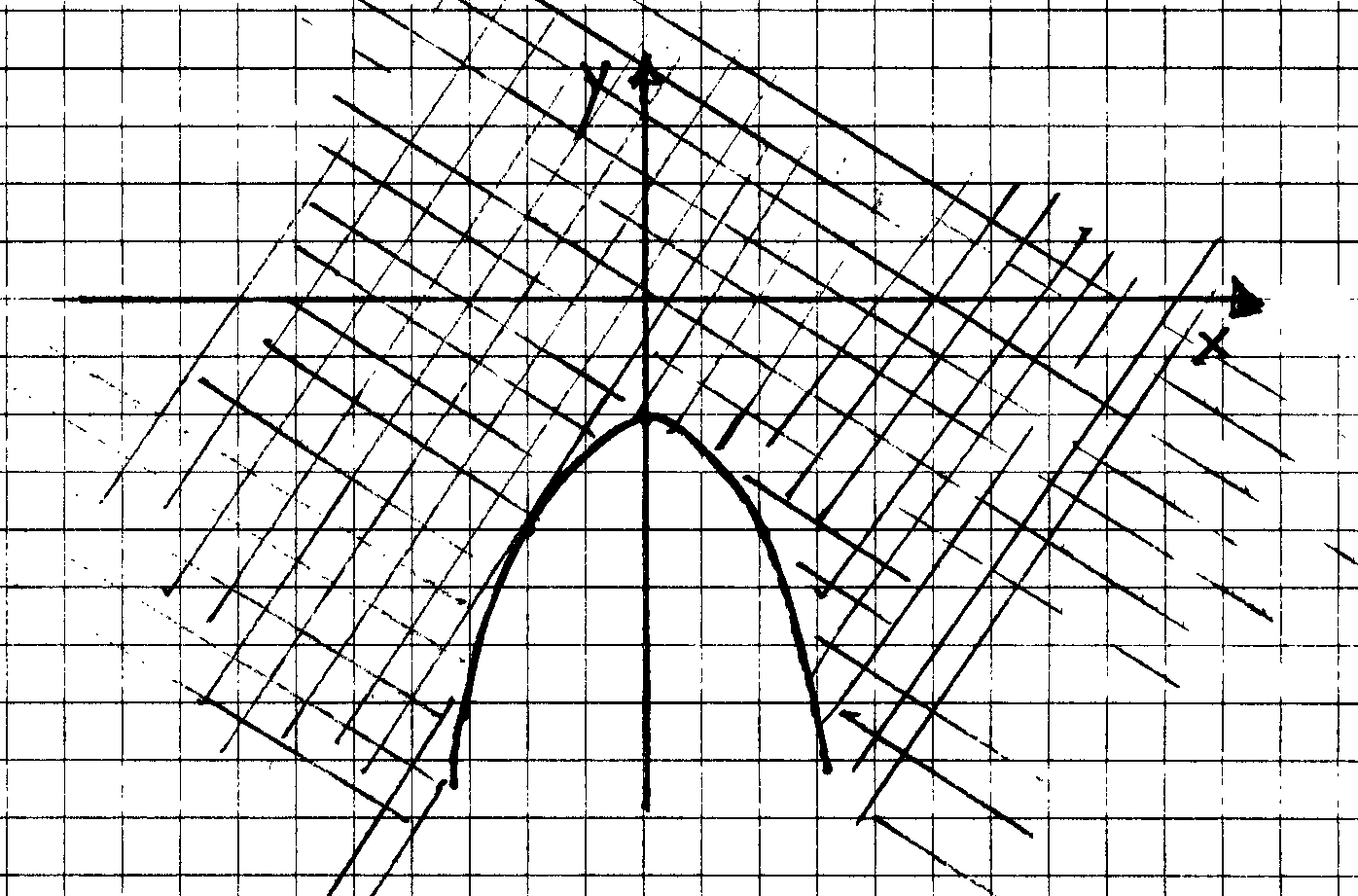
    Quindi
    Dom(f)0 = {(x,y) Î R2 t.c. y > -2-x2},
    [`(Dom(f))] = Dom(f),
    (Dom(f)){(x,y) Î R2 t.c. y = -2-x2} e
    D(Dom(f)) = Dom(f).
    (b) Il dominio della funzione si ottiene risolvendo la disequazione y+2-x2 ³ 0 (l'esponenziale, in quanto sempre positivo è ininfluente ai fini dell'esistenza della funzione). Il grafico:
     
     

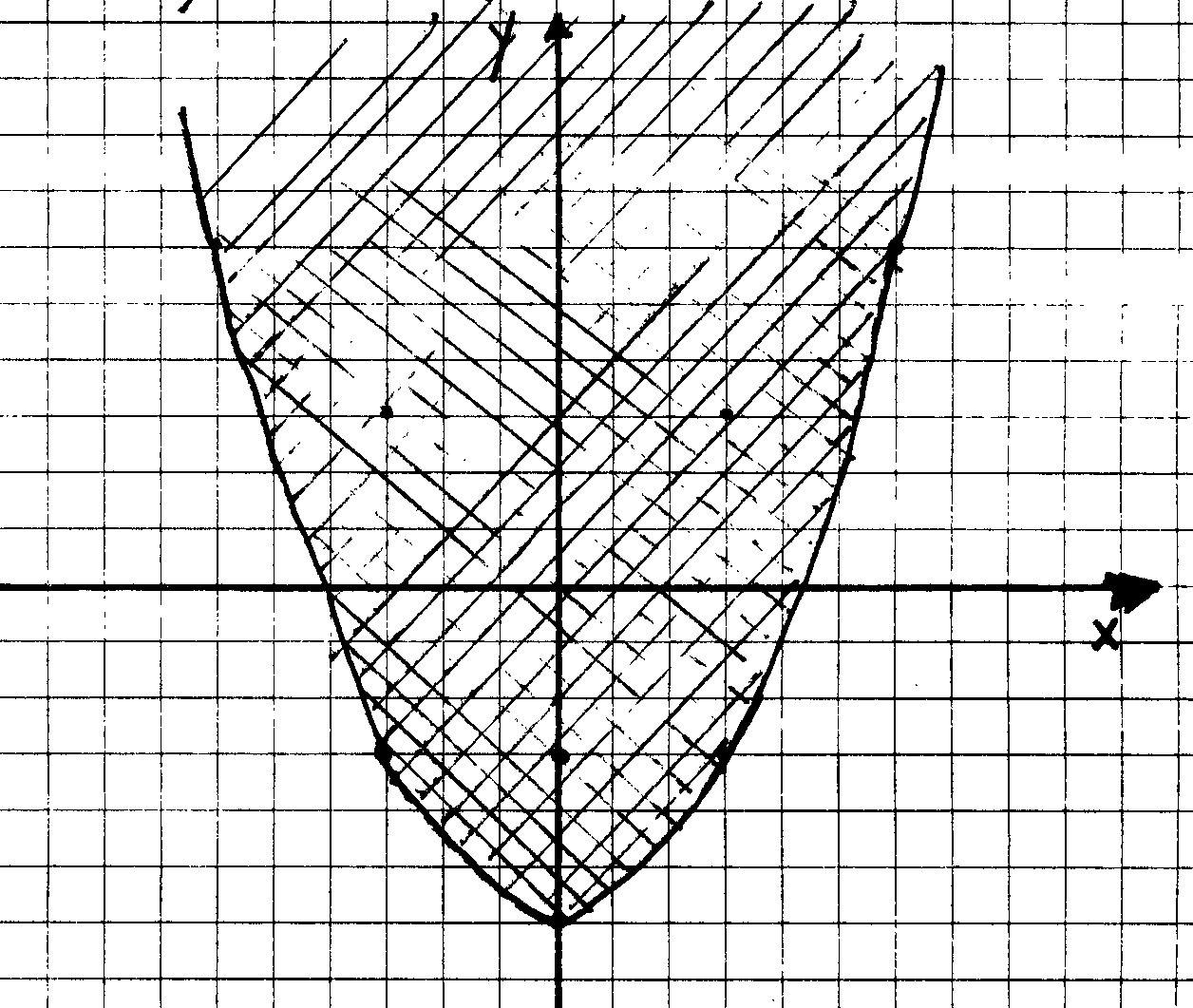
    Quindi
    Dom(f)0 = {(x,y) Î R2 t.c. y > -2+x2},
    [`(Dom(f))] = Dom(f),
    (Dom(f)){(x,y) Î R2 t.c. y = -2+x2} e
    D(Dom(f)) = Dom(f).

  5. Dopo averne tracciato la figura, si dimostri che il seguente sottoinsieme di R2 non è compatto costruendo un ricoprimento di aperti che non ammette un sottoricoprimento finito.
    6. S = {(x,y) Î R2 t.c. y Î [0,2] e y > x2}
     
    SOLUZIONE: La figura è la seguente:
     
     

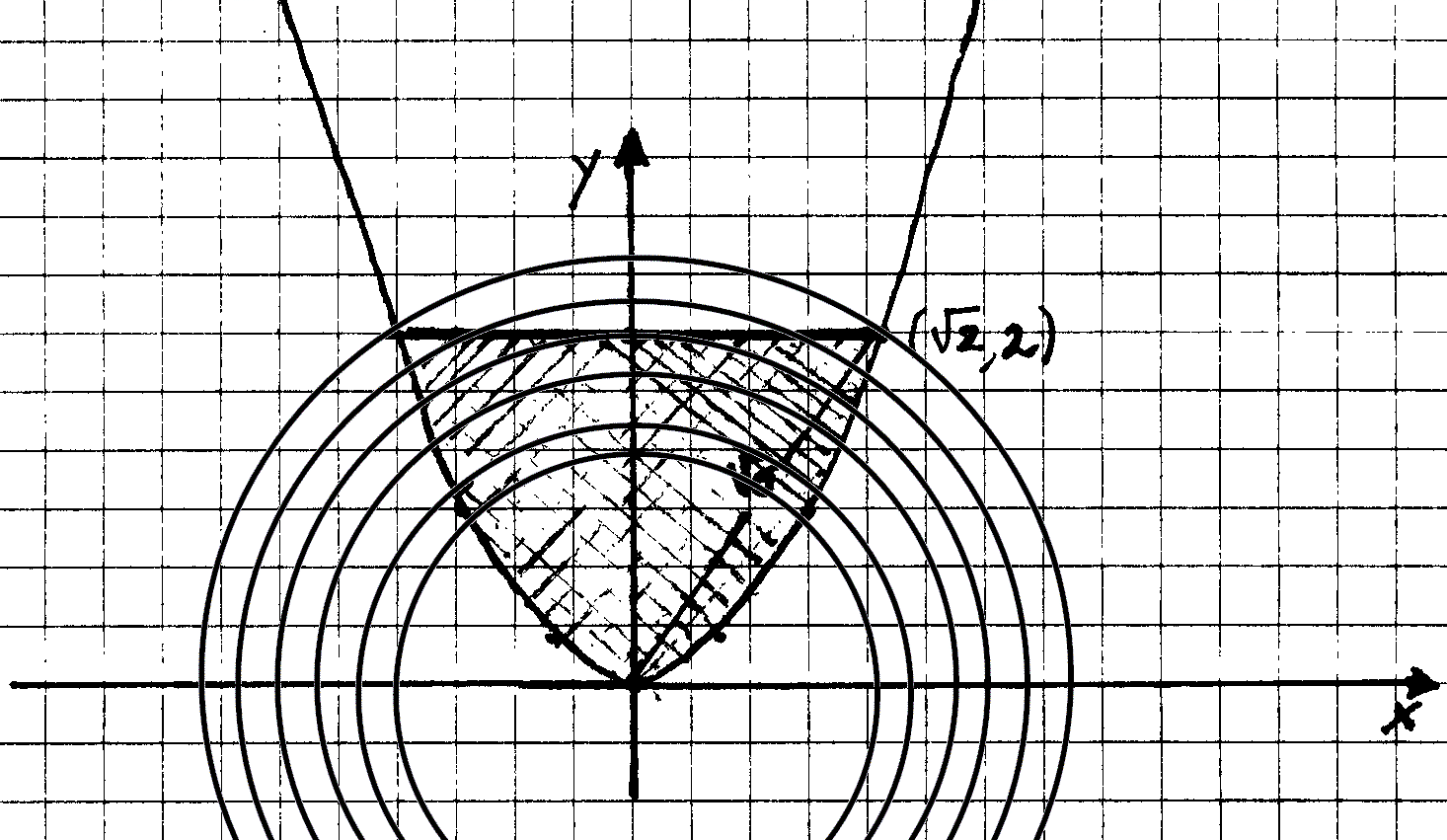
    Si consideri la seguente famiglia:

    {DÖ6-1/n((0,0))}n Î N.
     
    È necessario verificare che:
    1. La famiglia è un ricoprimento cioè che S Ì Èn Î NDÖ6-1/n((0,0))
    2 Il ricoprimento non ammette un sottoricoprimento finito cioè (essendo il ricoprimento telescopico) che per ogni n0 Î N,
    S\not Í DÖ6-1/n((0,0)).
     
    Per verificare 1. basta osservare che se (a,b) Î S, allora esiste d > 0 tale che a2+b2 = Ö6-d e quindi (a,b) Î DÖ6-1/n((0,0)) per tutti gli n > [1/( d)].
    Per verificare 2. basta osservare che il punto (Ö{(Ö6-[1/( n0)])2-4},2) Î S non appartiene a DÖ6-[1/( n0)]((0,0)) qualunque sia n0 Î N.
  6. Si discuta la continuità della seguente funzione f:R2®R:
    7. (a) f(x,y) =  ì 
    ï 
    ï 
    ï 
    í 
    ï 
    ï 
    ï 
    î 
    xyarctanx 
    y2+(arctanx)2
     
    se  (x,y) ¹ (0,0)
     
     
    0
     
    se  (x,y) = (0,0)
     
     
     
     
    (b) g(x,y) =  ì 
    ï 
    ï 
    ï 
    í 
    ï 
    ï 
    ï 
    î 
    xyarctany 
    x2+(arctany)2
     
    se  (x,y) ¹ (0,0)
     
     
    0
     
    se  (x,y) = (0,0)
     
     
     
    SOLUZIONE: (a) La funzione è sicuramente continua per tutti i valori di (x,y) per cui non si annulla il denominatore y2+(arctanx)2. Quest'ultimo si annulla esclusivamente per (x,y) = (0,0). Adesso utilizzando la disuguaglianza |ab|/(a2+b2) £ 1, otteniamo che per (x,y) ¹ (0,0), |f(x,y)| £ |x|. Con il metodo del confronto otteniamo che f(x,y) è continua anche in (0,0).
    (b) La soluzione è la stessa di quella di (a) osservando che g(x,y) = f(y,x).
  7. Si calcoli il differenziale e il piano tangente nel punto (1,1,eln2) della superficie di equazione z = exln(y+1).

    8. SOLUZIONE: Il gradiente della funzione è Ñf = (exln(y+1),ex/(y+1)) e quindi Ñf(1,1) = (eln2,e/2). Quindi per ogni x = (x1,x2) Î R2, abbiamo
    df(1,1)(x) = e(ln2·x1+ 1 
    2    		 x2).
     
    oppure usando la notazione che utilizza i differenziali delle proiezioni: df(1,1) = eln2dx+e/2dy. L'equazione del piano tangente in (1,1) è z = eln2+eln2(x-1)+e/2(y-1).
  8. Si calcoli il polinomio di Taylor di grado tre intorno al punto (0,0) della funzione
    9. (a) f(x,y) = ln(x+y+1).
     
     
    (b) f(x,y) = ln(x+y+1).
     
    SOLUZIONE:(a) È facile vedere che xf = yf = (x+y+1)-1 e quindi x2f = y2f = xyf = -(x+y+1)-2 e infine x3f = y3f = xy2f = x2yf = 2(x+y+1)-3 Sostituendo (x,y) = (0,0) otteniamo
    P3(x,y) = x+y- 1 
    2    		 (x2+2xy+y2)+ 1 
    3    		 (x3+3x2y+3xy2+y3).
     
     

    (b) È facile vedere che xf = -yf = (x-y+1)-1 e quindi x2f = y2f = -xyf = -(x-y+1)-2 e infine x3f = -y3f = xy2f = -x2yf = 2(x+y+1)-3 Sostituendo (x,y) = (0,0) otteniamo

    P3(x,y) = x-y- 1 
    2    		 (x2-2xy+y2)+ 1 
    3    		 (x3-3x2y+3xy2-y3).
     
  9. Sia
    10. (a) f(x,y) = y3-3y+x3-12x.
     
     
    (b) f(x,y) = y3-3y-x3+12x.
     
    Determinare i punti critici di f e classificarli con il metodo della matrice Hessiania.
    SOLUZIONE:(a) Il gradiente della funzione è dato da Ñf = (3x2-12,3y2-3) che si annulla nei seguenti quattro punti:
    A(2,1)  B(2,-1)  C(-2,1)  D(-2,-1).
     
    La matrice Hessiana è data da
    æ 
    ç 
    è 
    6x
     
    0
     
    0
     
    6y
     
         		 ö 
    ÷ 
    ø     		 .
     
    Quindi A è un massimo, D è un minimo e B e C non sono né massimi né minimi.
    (b) Il gradiente della funzione è dato da Ñf = (-3x2+12,3y2-3) che si annulla nei seguenti quattro punti:
    A(2,1)  B(2,-1)  C(-2,1)  D(-2,-1).
     
    La matrice Hessiana è data da
    æ 
    ç 
    è 
    -6x
     
    0
     
    0
     
    6y
     
         		 ö 
    ÷ 
    ø     		 .
     
    Quindi B è un massimo, C è un minimo e A e D non sono né massimi né minimi.
  10. Si risolva la seguente equazione differenziale:
    11. (a) (cos(x+y)+cosx)dx+(cosy+cos(x+y))dy = 0
     
     
    (b) (cos(x-y)+cosx)dx+(cosy-cos(x-y))dy = 0
     
    SOLUZIONE(a) Si tratta di un equazione differenziale esatta in quanto
    ¶ 
    y    		 (cos(x+y)+cosx) =  ¶ 
    x    		 (cosy+cos(x+y)) = -sin(x+y).
     
    Integrando il primo coefficiente rispetto a x, otteniamo
    ó 
    õ     		 (cos(x+y)+cosx)dx = sin(x+y)+sinx+g(y)
     
    e derivando rispetto a y otteniamo
    cos(x+y)+g¢(y) = cos(x+y)+cosy.
     
    Quindi g(y) = siny +c e la soluzione generale è
    sin(x+y)+sinx+siny = -c.
     
    (b) Si tratta di un equazione differenziale esatta in quanto
    ¶ 
    y    		 (cos(x-y)+cosx) =  ¶ 
    x    		 (cosy-cos(x-y)) = sin(x-y).
     
    Integrando il primo coefficiente rispetto a x, otteniamo
    ó 
    õ     		 (cos(x-y)+cosx)dx = sin(x-y)+sinx+g(y)
     
    e derivando rispetto a y otteniamo
    -cos(x-y)+g¢(y) = -cos(x-y)+cosy.
     
    Quindi g(y) = siny +c e la soluzione generale è
    sin(x-y)+sinx+siny = -c.
     
     
File translated from TEX by TTH, version 1.94.
On 23 Nov 1998, 14:36.