Analitica- una funzione
Coercitiva- una funzione
![]() si dice coercitiva se
si dice coercitiva se
![]()
In questo caso un corollario del teorema di Weierstrass assicura l'esistenza
di minimi per f in insiemi chiusi (anche non limitati) a patto
che f sia continua (o anche semicontinua inferiormente).
Consistente- un metodo ad un passo per Equazioni Differenziali
Ordinarie si dice consistente con ordine p se, definito ![]() tramite l'equazione
tramite l'equazione
![]()
e y(x) come la soluzione di
![]()
si ha
![]() .
Nel caso di metodi a piú passi, l'analoga
proprietá si esprime come
.
Nel caso di metodi a piú passi, l'analoga
proprietá si esprime come
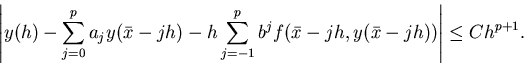
Convessa- una funzione
![]() si dice convessa se per ogni
coppia di punti
si dice convessa se per ogni
coppia di punti
![]() e per ogni
e per ogni
![]() si ha
si ha
![]()
e strettamente convessa se la disuguaglianza precedente é stretta. Una
funzione C2 é convessa se e solo se la sua matrice hessiana é sempre
semidefinita positiva; se poi la hessiana é sempre definita positiva allora
la funzione é strettamente convessa (in questo caso non vale il viceversa).
Definita positiva (negativa)- una matrice simmetrica A si dice definita positiva (negativa) se
per ogni ![]() .
Se la disuguaglianza precedente é soddisfatta
eventualmente con il segno di uguaglianza la matrice si dice semidefinita
positiva (negativa). Se nessuno di questi casi é soddisfatto, allora la
matrice si dice indefinita. Se A é definita positiva (negativa),
allora ha autovalori tutti reali positivi (negativi); se é semidefinita,
allora ha anche autovalori nulli; se é indefinita puó avere autovalori
(reali) positivi, negativi o nulli.
.
Se la disuguaglianza precedente é soddisfatta
eventualmente con il segno di uguaglianza la matrice si dice semidefinita
positiva (negativa). Se nessuno di questi casi é soddisfatto, allora la
matrice si dice indefinita. Se A é definita positiva (negativa),
allora ha autovalori tutti reali positivi (negativi); se é semidefinita,
allora ha anche autovalori nulli; se é indefinita puó avere autovalori
(reali) positivi, negativi o nulli.
Densa- una famiglia numerabile di funzioni
![]() si dice densa in uno spazio funzionale
X se per ogni
si dice densa in uno spazio funzionale
X se per ogni ![]() ed ogni
ed ogni
![]() esiste un intero N tale che
si abbia
esiste un intero N tale che
si abbia
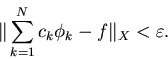
Dominante diagonale- una matrice A si dice dominante diagonale per
righe (per colonne) se
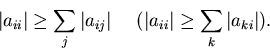
Se la disuguaglianza é soddisfatta con il segno stretto, la matrice si dice
strettamente dominante diagonale (rispettivamente per righe o per
colonne).
Integrabile- una funzione
![]() si dice Riemann-integrabile
se, costruita una generica decomposizione
si dice Riemann-integrabile
se, costruita una generica decomposizione
![]() di [a,b],
al variare di N e degli N+1 punti
di [a,b],
al variare di N e degli N+1 punti
![]() ,
le sue somme
integrali soddisfano la condizione
,
le sue somme
integrali soddisfano la condizione
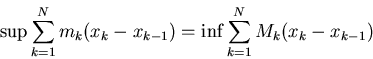
dove
![]()
Norma- una norma ![]() é una applicazione da uno spazio vettoriale
X in R che soddisfa le seguenti proprietá:
é una applicazione da uno spazio vettoriale
X in R che soddisfa le seguenti proprietá:
![]()
![]()
![]()
Se X é lo spazio degli operatori lineari limitati su uno spazio vettoriale
Y, allora si richiede di regola che la norma soddisfi anche le ulteriori
proprietá
![]()
![]()
e si indica come norma naturale (associata ad una certa norma su Y) la
seguente norma su X:
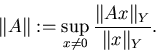
Numero di condizionamento- data una matrice nonsingolare A ed una
norma matriciale ![]() ,
si indica come numero di condizionamento di
A il numero reale positivo
,
si indica come numero di condizionamento di
A il numero reale positivo
![]()
Si ha che ![]() .
Se K(A) é molto grande la matrice A ed il sistema
lineare associato si dicono malcondizionati. Nel caso di sistemi nonlineari
tipicamente si indicano come malcondizionati sistemi in cui sia tale la matrice
Jacobiana del sistema.
.
Se K(A) é molto grande la matrice A ed il sistema
lineare associato si dicono malcondizionati. Nel caso di sistemi nonlineari
tipicamente si indicano come malcondizionati sistemi in cui sia tale la matrice
Jacobiana del sistema.
Ortogonali- le funzioni di una famiglia
![]() si dicono
mutuamente ortogonali rispetto ad un prodotto scalare
si dicono
mutuamente ortogonali rispetto ad un prodotto scalare
![]() se
se
![]()
Pieno - si indica come piena una matrice con un numero
di elementi
non nulli dello stesso ordine del numero totale di elementi della matrice,
ovvero O(n2) al variare della dimensione n. Il corrispondente sistema
lineare si indicherá come sistema pieno.
Polinomi di Chebyshev- si indica con questo nome la famiglia di polinomi
definiti in modo ricorsivo da
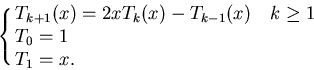
Tali polinomi sono mutuamente ortogonali in
L2w([-1,1]) rispetto al peso
w(x)=(1-x2)-1/2, piú precisamente
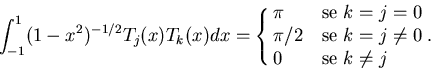
Polinomi di Legendre- si indica con questo nome la famiglia di polinomi
definiti in modo ricorsivo da
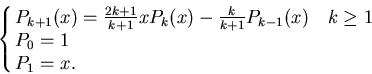
Tali polinomi sono mutuamente ortogonali in
L2([-1,1]), e piú precisamente
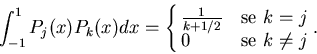
Prodotto scalare- si dice prodotto scalare su uno spazio vettoriale Xuna applicazione
![]() tale che
tale che
![]()
![]()
Si dice norma associata al prodotto scalare
![]() la norma
definita da
la norma
definita da
![]()
Sistema trigonometrico- si dice sistema trigonometrico relativo ad un
intervallo [0,T] il sistema di funzioni
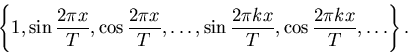
Tale famiglia é densa nello spazio
L2([0,T]).
Sparso- si indica come sparsa una matrice con un numero di elementi
non nulli piccolo rispetto al numero totale di elementi della matrice,
ovvero o(n2) al variare della dimensione n. Il corrispondente sistema
lineare si indicherá come sistema sparso. Un caso notevole é quello
delle matrici a banda per cui si ha che il numero di elementi non nulli é
O(n).
Stabilitá- uno schema numerico per Equazioni Differenziali Ordinarie
si dice stabile se perturbazioni piccole dei dati iniziali producono
perturbazioni piccole della soluzione. Piú formalmente, fissati x>x0,
![]() e due dati inziali y0 e
e due dati inziali y0 e ![]() tali che
tali che
![]() ,
si ha per le corrispondenti soluzioni:
,
si ha per le corrispondenti soluzioni:
![]()
per ogni
![]() ,
con C dipendente da x e
,
con C dipendente da x e
![]() ma
non da h. Nel caso lineare ció corrisponde alla equilimitatezza delle
soluzioni discrete al variare di h su tutto l'intervallo [x0,x].
ma
non da h. Nel caso lineare ció corrisponde alla equilimitatezza delle
soluzioni discrete al variare di h su tutto l'intervallo [x0,x].
Stabilitá assoluta- uno schema numerico per Equazioni Differenziali
Ordinarie si dice assolutamente stabile se, applicato al problema modello
![]()
con ![]() ,
produce una successione uk che soddisfa la condizione
,
produce una successione uk che soddisfa la condizione
![]()
ovvero se conserva la proprietá qualitativa di stabilitá delle soluzioni
del problema modello. Tale condizione include quella di stabilitá data
precedentemente.
![]()
![]()
Up: No Title
Previous: Esercizi interattivi
Roberto Ferretti e Tiziana Manfroni - 1999