Data una funzione f(x), di cui sia disponibile una approssimazione come
combinazione lineare di funzioni
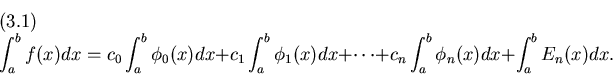
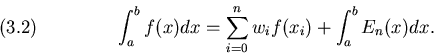

Risultati fondamentali
![]() Se le
Se le ![]() sono la base di Lagrange, i nodi sono equidistanti
con passo h,
[x0,xn]=[a,b] (oppure x0=a+h, xn=b-h), allora il grado
di precisione della quadratura é n se n é dispari, n+1 se n é
pari. Tali formule di quadratura si indicano come quadrature di
Newton-Cotes, chiuse se
[x0,xn]=[a,b], aperte altrimenti.
sono la base di Lagrange, i nodi sono equidistanti
con passo h,
[x0,xn]=[a,b] (oppure x0=a+h, xn=b-h), allora il grado
di precisione della quadratura é n se n é dispari, n+1 se n é
pari. Tali formule di quadratura si indicano come quadrature di
Newton-Cotes, chiuse se
[x0,xn]=[a,b], aperte altrimenti.
![]() Se
Se ![]() ,
allora wi>0 per ogni
,
allora wi>0 per ogni ![]() ,
e
,
e
![]() .
Se n>6, allora esistono coefficienti wi<0 per qualche
.
Se n>6, allora esistono coefficienti wi<0 per qualche ![]() ,
e
,
e
![]() .
.
![]() Se le
Se le ![]() sono la base associata ad una interpolazione
composita di grado fissato, e f é Riemann-integrabile, allora
sono la base associata ad una interpolazione
composita di grado fissato, e f é Riemann-integrabile, allora
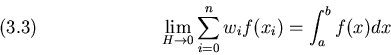
![]() Se i nodi di interpolazione sono gli zeri di un polinomio di
Legendre di grado n+1 e le
Se i nodi di interpolazione sono gli zeri di un polinomio di
Legendre di grado n+1 e le ![]() sono la base di Lagrange associata a
questa scelta di nodi, allora la quadratura ha grado di precisione 2n+1 e per
ogni n>1 ed
sono la base di Lagrange associata a
questa scelta di nodi, allora la quadratura ha grado di precisione 2n+1 e per
ogni n>1 ed ![]() ,
si ha wi>0.
,
si ha wi>0.