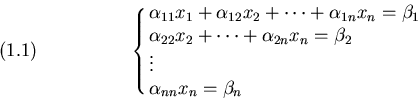
Il metodo di eliminazione di Gauss e la fattorizzazione LU.

Il metodo di eliminazione di Gauss e' in genere noto dai corsi precedenti. Ne richiamiamo comunque brevemente la filosofia. Intanto, dato un sistema triangolare

$$\cases{ \alpha_{11}x_1+\alpha_{12}x_2+\cdots+\alpha_{1n}x_n=\... ...beta_2 \cr \vdots \cr \alpha_{nn}x_n=\beta_n \cr } \leqno(1.1)$$

la sua soluzione si puo' calcolare tramite le cosiddette sostituzioni all'indietro come

$$x_n={b_n\over \alpha_{nn}}$$

$$x_k={1\over \alpha_{kk}}\left(b_k-\sum_{j=k+1}^n \alpha_{kj}x_j\right) ~~~(k=n-1,\ldots,1) \leqno(1.2)$$

in cui il valore di una incognita viene ottenuto sulla base di quelle (successive) giá calcolate.

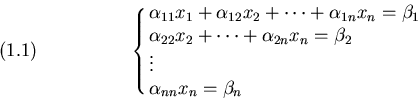
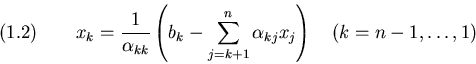
La logica del metodo di eliminazione e' di riportare un generico sistema quadrato

$$\cases{ a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1 \cr a_{21}x_... ...\cr a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n=b_n \cr } \leqno(1.3)$$

alla forma del sistema triangolare (1.1). Per fare ció, si parte da x₁sommando alla riga k-esima la prima moltiplicata per -a_k1/a₁₁. Alla fine di n-1 combinazioni lineari cosí costruite, la variabile x₁ sará prestente solo nella prima equazione. Si riparte quindi dalla variabile x₂con la stessa modalitá (meno che per il fatto che le combinazioni lineari si effettuano sulle righe dalla terza in poi), e cosí via. Il risultato é un sistema triangolare nella forma (1.1) che puó essere risolto per sostituzioni all'indietro.

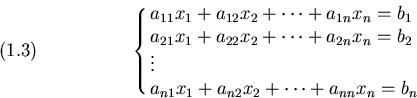
Risultati fondamentali

$\bullet$ Se la matrice A del sistema (1.3) é nonsingolare, esiste una permutazione delle equazioni per cui questo algoritmo puó essere completato. Il vettore che si ottiene dalla sostituzione all'indietro (1.2) é la unica soluzione del sistema (1.3).

$\bullet$ La permutazione di righe che rende piú stabile l'algoritmo é quella in cui al passo di eliminazione della variabile k-esima viene portata in k-esima posizione l'equazione in cui il coefficiente della variabile che viene eliminata é massimo (strategia di pivoting parziale).

$\bullet$ Se la matrice A é a diagonale dominante o definita positiva, allora l'algoritmo puó essere completato senza permutazione delle righe.

$\bullet$ Se la matrice A del sistema (1.3) é nonsingolare, esiste una permutazione delle equazioni che permette di scrivere A=LU con Ltriangolare inferiore, U triangolare superiore (tale permutazione coincide con quella che permette l'esecuzione dell'algoritmo di eliminazione). La soluzione del sistema (1.3) si ottiene dalla successiva soluzione dei due sistemi triangolari Lz=b e Ux=z.

$\bullet$ Se la matrice A é definita positiva, allora si puó fattorizzare nella forma A=LL^t con L triangolare inferiore.