Sistemi di equazioni lineari e nonlineari.

Nel caso generale, il problema che si pone é di risolvere un sistema di equazioni della forma

$$F(x)=0.~~~~(F:R^n\to R^n) \leqno(SEN)$$

Come é noto, non esistono risultati di esistenza e molteplicitá di soluzioni per questo problema, meno che in situazioni particolari (teorema degli zeri in R, teoremi di punto fisso in spazi metrici completi).

Nel caso in cui F sia lineare, il sistema si scrive nella forma estesa

$$\cases{ a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1 \cr a_{21}x_... ...\cr a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n=b_n \cr } \leqno(SEL)$$

o in forma compatta Ax=b. In questo caso é noto che il sistema é risolubile a patto che la matrice A sia nonsingolare, ed esitono algoritmi risolutivi che possono essere completati in un numero finito di passi.

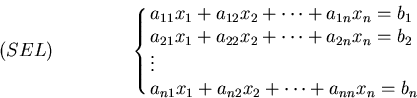
Le strategie piú comuni di soluzione numerica di questo problema sono di tre tipi: metodi diretti, iterativi e di minimizzazione.

Metodi diretti - Si applicano solo al problema lineare (SEL). Consentono di arrivare alla soluzione con un numero finito di operazioni, a patto di operare in aritmetica esatta. In genere, si ritengono convenienti per sistemi lineari pieni e relativamente di piccole dimensioni. Occupano piú memoria degli altri metodi e soffrono una maggiore instabilitá.

Metodi iterativi - Si possono applicare sia al problema lineare che a quello nolineare. Generano successioni che, sotto opportune ipotesi, convergono ad una soluzione del sistema. In generale la soluzione non viene raggiunta in un numero finito di passi, quindi nei sistemi lineari possono essere meno precisi (a paritá di numero di operazioni), a meno che non vengano applicati a problemi sparsi . Occupano peró meno memoria e sono piú stabili dei metodi diretti.

Metodi di minimizzazione - Sono metodi iterativi che sotto ipotesi opportune convergono al minimo di una funzione $f:R^n\to R$. Se si puó trovare una funzione f tale che $F(x)=\nabla f(x)$, e se f ha minimo (nel caso dei sistemi lineari, se A é definita positiva si puó porre f(x)=1/2 (Ax,x)-(b,x)), si possono applicare alla soluzione di (SEN) o (SEL). Una maniera standard di applicarli consiste nel porre f(x)=F(x)^tF(x), il che corrisponde alla strategia del minimo residuo. I metodi di minimizzazione hanno tutte le caratteristiche dei metodi iterativi; sono particolarmente efficienti se F é giá nella forma di un gradiente. Se invece si minimizza il residuo, allora sia a causa della eventuale mancanza di convessitá di f, sia a causa del condizionamento , possono essere meno competitivi.