Metodi iterativi di minimizzazione libera.

Si tratta di algoritmi di risoluzione del problema

$$\min_{x\in R^n} f(x) \leqno(3.1)$$

con $f\in C^1$ (per i metodi di tipo Newton $f\in C^2$). Ricordiamo che nel caso f sia strettamente convessa il punto di minimo in (3.1) esiste ed é l'unico punto stazionario, e quindi questo problema equivale a trovare la soluzione del sistema nonlineare

$$\nabla f(x)=0.$$

Se f é quadratica definita positiva, ovvero f(x)=1/2(Ax,x)-(b,x) con Adefinita positiva, allora il punto di minimo é soluzione del sistema lineare Ax=b.

La struttura generale di un metodo iterativo di minimizzazione é

$$x_{k+1}=x_k - \beta_k d_k, \leqno(3.2)$$

dove $\beta_k\in R^+$, $d_k\in R^n$ ed x₀ é assegnato. Si tratta quindi di muoversi lungo la direzione d_k con passo $\beta_k$, entrambi da scegliersi opportunamente ad ogni passo. Di regola si richiede che la direzione d_k sia una direzione di discesa, ovvero che $(d_k,\nabla f(x_k))<0$, e che inoltre f(x_k+1)<f(x_k).

Le strategie piú comuni per scegliere le direzioni d_k sono:

Discesa piú ripida (o gradiente) - si sceglie $d_k=-\nabla f(x_k)$. Questo equivale alla direzione in cui la derivata direzionale di f é di modulo maggiore.

Rilassamento - si sceglie $d_k=\pm e_j~(j=k({\rm mod}~n))$, ovvero ci si muove lungo le direzioni coordinate prese in sequenza. Nel caso di funzioni quadratiche si riottiene l'algoritmo di Gauss-Seidel.

Direzioni coniugate - Nel caso di una f quadratica definita positiva, si scelgono le direzioni d_k in modo tale che

$$(Ad_k,d_j)\cases{>0 & se $k=j$\cr =0 & se $k\not=j$\cr} \leqno(3.3)$$

(esistono opportune generalizzazioni nel caso di funzioni non quadratiche).

Newton - si sceglie $d_k=-P_k\nabla f(x_k)$ con P_k=H_f(x_k)^-1 (H_f matrice hessiana di f) nel caso del metodo di Newton propriamente detto, ed una sua opportuna versione approssimata nel caso dei metodi Quasi-Newton.

Le strategie piú comuni per scegliere gli scalari $\beta_k$ sono:

Passo fisso - In questo caso si sceglie $\beta_k\equiv\beta$ (costante).

Ricerca esatta - Si sceglie $\beta_k$ in modo che si abbia

$$f(x_k+\beta_kd_k)=\min_\beta f(x_k+\beta d_k) \leqno(3.4)$$

applicando un metodo di ricerca unidimensionale, ad esempio il metodo di bisezione. Nel caso di funzioni quadratiche il minimo (3.4) si puó calcolare esplicitamente.

Ricerca parziale (criterio di Goldstein) - In questo caso $\beta_k$ é determinato (in modo non univoco) dalla condizione

$$f(x_k)+\sigma_1\beta_k(d_k,\nabla f(x_k)) \le f(x_k+\beta_kd_k)\le f(x_k)+\sigma_2\beta_k(d_k,\nabla f(x_k)) \leqno(3.5)$$

dove $0<\sigma_2<\sigma_1<1$.

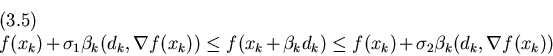
Risultati fondamentali

$\bullet$ Se f(x) é differenziabile, strettamente convessa e coercitiva, il metodo di rilassamento con ricerca esatta é convergente per ogni scelta di $x_0\in R^n$.

$\bullet$ Se f(x) ha gradiente lipschitziano e la successione x_ké generata tramite l'algoritmo del gradiente (sia con ricerca esatta che parziale), allora tutte le sottosuccessioni convergenti di x_k convergono a punti stazionari di f. Se f é strettamente convessa e coercitiva, allora tutta la successione x_k converge (linearmente) all'unico punto di minimo di f. Lo stesso risultato vale per il metodo a passo fisso, a patto che il passo $\beta$ sia sufficientemente piccolo.

$\bullet$ Se f(x) é quadratica e definita positiva, il metodo delle direzioni coniugate con ricerca esatta converge al piú in n passi al punto di minimo.

$\bullet$ Se $f(x)\in C^2$ e H_f é definita positiva in un intorno del minimo $\bar x$, allora esiste un intorno U di $\bar x$ tale che, se $x_0\in U$, la successione x_k generata dall'algoritmo di Newton converge quadraticamente a $\bar x$.