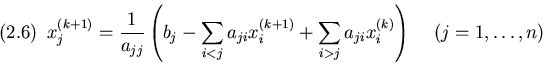Dato il sistema di n equazioni, lineari o nonlineari,
Nel caso la successione x(k) converga ad un certo ![]() ,
si caratterizza
la velocitá di convergenza tramite il piú grande esponente
,
si caratterizza
la velocitá di convergenza tramite il piú grande esponente ![]() che
permette di verificare la disuguaglianza
che
permette di verificare la disuguaglianza
Risultati fondamentali
![]() Se esiste un insieme chiuso
Se esiste un insieme chiuso
![]() tale
che
tale
che
![]() e che
e che
![]() per ogni
per ogni ![]() con L<1, allora l'equazione (2.2) ha soluzione unica
con L<1, allora l'equazione (2.2) ha soluzione unica ![]() in E, e
se
in E, e
se
![]() ,
allora
,
allora
![]() .
La convergenza di x(k)verso x é (almeno) lineare.
.
La convergenza di x(k)verso x é (almeno) lineare.
![]() Se n=1, allora l'equazione F(x)=0 si puó sempre porre
nella forma (2.2) ponendo
Se n=1, allora l'equazione F(x)=0 si puó sempre porre
nella forma (2.2) ponendo
![]() .
Se esiste una radice
.
Se esiste una radice ![]() e
e
![]() ,
allora la successione x(k) converge
quadraticamente a
,
allora la successione x(k) converge
quadraticamente a ![]() per ogni x(0) in un opportuno intorno di
per ogni x(0) in un opportuno intorno di ![]() .
.
![]() Se il sistema (2.1) é lineare, ovvero F(x)=Ax-b, allora
si puó definire la iterazione (2.3) nella forma (metodo di Jacobi):
Se il sistema (2.1) é lineare, ovvero F(x)=Ax-b, allora
si puó definire la iterazione (2.3) nella forma (metodo di Jacobi):
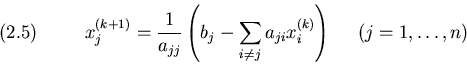
![]() Se in (2.5) si sceglie di utilizzare nella stessa iterazione
le variabili appena calcolate, si ottiene lo schema (metodo di
Gauss-Seidel):
Se in (2.5) si sceglie di utilizzare nella stessa iterazione
le variabili appena calcolate, si ottiene lo schema (metodo di
Gauss-Seidel):