Diamo inizialmente due espressioni facilmente calcolabili del polinomio interpolatore relativo a n+1 punti.
Data una funzione f(x) e n+1 punti (detti nodi dell'interpolazione)
![]() ,
intendiamo trovare un polinomio (interpolatore)
,
intendiamo trovare un polinomio (interpolatore) ![]() di
grado al piú n tale che:
di
grado al piú n tale che:
Tale polinomio esiste ed é unico. Se ne possono dare diverse forme, le due principali sono la forma di Lagrange e quella di Newton.
Polinomio di Lagrange - Nella forma di Lagrange, il
polinomio ![]() si esprime come:
si esprime come:
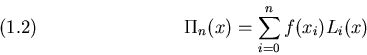
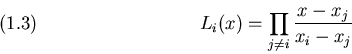
Polinomio di Newton - Nella forma di Newton, il
polinomio interpolatore si scrive:
![\begin{displaymath}\Pi_n(x) = f[x_0] + f[x_0,x_1](x-x_0) + \cdots + f[x_0,\ldots,x_n]
(x-x_0)\cdots(x-x_{n-1}).
\leqno(1.4)
\end{displaymath}](img63.gif)
![\begin{displaymath}f[x_0,\ldots,x_k] = {f[x_1,\ldots,x_k] - f[x_0,\ldots,x_{k-1}] \over x_k -
x_0},
\leqno(1.5a)
\end{displaymath}](img65.gif)
Nei problemi di interpolazione, la convergenza del polinomio interpolatore a
f dipende dalla regolaritá della funzione e dalla legge con cui si
infittiscono i nodi. Ad esempio, come si vedrá nei risultati generali,
mantenendo i nodi equidistanti si ottiene convergenza solo per una classe di
funzioni molto ristretta.
Per ottenere precisioni crescenti nelle approssimazioni per interpolazione, si usano in pratica altre strategie:
Nodi Chebyshev - In questa strategia, i nodi sono
posizionati negli zeri di un polinomio di
Chebyshev di grado n+1. Nel caso
dei nodi di Chebyshev-Gauss-Lobatto si scelgono i nodi
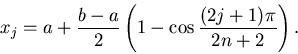
Interpolazioni composite - Suddividendo l'intervallo
di interpolazione [a,b] in sottointervalli di ampiezza ![]() contenenti
ognuno n+1 nodi di interpolazione (n-1 interni, piú due agli estremi in
comune con gli intervalli adiacenti) per ogni sottointervallo, si ottiene una
interpolazione polinomiale di ordine n a tratti. In ogni sottointervallo i
nodi sono in genere equidistanti.
contenenti
ognuno n+1 nodi di interpolazione (n-1 interni, piú due agli estremi in
comune con gli intervalli adiacenti) per ogni sottointervallo, si ottiene una
interpolazione polinomiale di ordine n a tratti. In ogni sottointervallo i
nodi sono in genere equidistanti.
Risultati fondamentali
![]() Se
Se
![]() e
e
![]() ,
allora l'errore di approssimazione si puó rappresentare come:
,
allora l'errore di approssimazione si puó rappresentare come:
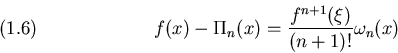
![]() Se f é analitica in
I, allora per
Se f é analitica in
I, allora per
![]() si ha
si ha
![]() per ogni
per ogni ![]() ,
comunque si scelgano n nodi distinti.
In particolare, questo é vero se
xi=i(b-a)/n (nodi equidistanti).
,
comunque si scelgano n nodi distinti.
In particolare, questo é vero se
xi=i(b-a)/n (nodi equidistanti).
![]() Se
Se ![]() é costruito sui nodi di Chebyshev, il
polinomio
é costruito sui nodi di Chebyshev, il
polinomio
![]() che compare nell'espressione dell'errore (1.6) ha
norma minima in
che compare nell'espressione dell'errore (1.6) ha
norma minima in
![]() .Con questa scelta viene minimizzata la
stima di errore, derivata da (1.6),
.Con questa scelta viene minimizzata la
stima di errore, derivata da (1.6),
![\begin{displaymath}\vert f(x)-\Pi_n(x)\vert\le {1\over (n+1)!} \Vert f^{n+1}\Ver...
...^\infty([x_0,x_n])}
\Vert\omega_n\Vert _{L^\infty([x_0,x_n])}.
\end{displaymath}](img80.gif)
![]() Se
Se
![]()
![]() ,
il polinomio interpolatore
,
il polinomio interpolatore ![]() costruito sui nodi di Chebyshev converge a f(x) per
costruito sui nodi di Chebyshev converge a f(x) per
![]() ,
e vale la
stima
,
e vale la
stima
![]() per ogni
per ogni ![]() .
.
![]() Se
Se
![]() ,
l'interpolazione composita
,
l'interpolazione composita
![]() di grado n con passo H converge a f(x) e
di grado n con passo H converge a f(x) e
![]() per ogni
per ogni ![]() .
.