Equazioni Differenziali Ordinarie: metodi a piú passi

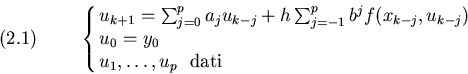
La approssimazione u_k+1 di y(x_k+1) si costruisce nei metodi a piú passi (o multistep) in base alle informazioni calcolate negli ultimi p passi, secondo lo schema generale:

$$\cases{u_{k+1}=\sum_{j=0}^p a_ju_{k-j}+h\sum_{j=-1}^pb^jf(x_{... ...k-j})\cr u_0=y_0\cr u_1,\ldots,u_p~~{\rm dati}\cr} \leqno(2.1)$$

in cui il calcolo dei primi p punti della soluzione si effettua tipicamente con un metodo ad un passo di ordine sufficientemente alto, o mediante sviluppo di Taylor. Lo schema (2.1) é detto schema a p+1 passi; se b_-1=0 si tratta di uno schema esplicito, mentre se $b_{-1}\not=0$ lo schema é implicito e u_k+1 va calcolato risolvendo l'equazione nonlineare (2.1).

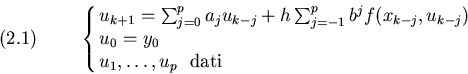
La classe piú utilizzata di metodi multistep é quella dei cosiddetti metodi di Adams per i quali a₀=1, $a_j=0~(j=1,\ldots,p)$, e che sono costruiti integrando su [x_k,x_k+1] il polinomio interpolatore relativo ai punti f(x_k-j,u_k-j). A seconda della natura esplicita o implicita del metodo, si possono dividere in due classi (a cui, per comoditá di esposizione, aggiungeremo una terza che ne rappresenta la combinazione):

Metodi di Adams-Bashforth - Per questi metodi b_-1=0 e quindi si tratta di metodi espliciti. Per p=0,1,2 si ottengono gli schemi:

$$u_{k+1}=u_k+hf(x_k,u_k)~~~~{\rm (Eulero)} \leqno(2.2)$$

$$u_{k+1}=u_k+h\left[{3\over 2}f(x_k,u_k)-{1\over 2}f(x_{k-1},u_{k-1})\right] \leqno(2.3)$$

$$u_{k+1}=u_k+h\left[{23\over 12}f(x_k,u_k) - {4\over 3}f(x_{k-1},u_{k-1}) - {5\over 12}f(x_{k-2},u_{k-2})\right] \leqno(2.4)$$

Metodi di Adams-Moulton - In questi metodi $b_{-1}\not=0$; si tratta perció di metodi impliciti. Per p=0,1,2 si ottiene:

$$u_{k+1}=u_k+hf(x_{k+1},u_{k+1})~~~~{\rm (Eulero~implicito)} \leqno(2.5)$$

$$u_{k+1}=u_k+h\left[{1\over 2}f(x_{k+1},u_{k+1})+{1\over 2}f(x_k,u_k)\right] ~~~~{\rm (Crank-Nicolson)} \leqno(2.6)$$

$$u_{k+1}=u_k+h\left[{5\over 12}f(x_{k+1},u_{k+1})+{2\over 3}f(x_k,u_k) - {1\over 12}f(x_{k-1},u_{k-1})\right] \leqno(2.7)$$

Metodi Predictor-Corrector - In questo caso il calcolo viene effettuato tramite un metodo di Adams-Moulton a p passi (corrector) in cui la approssimazione iniziale per la soluzione iterativa del metodo implicito viene fornita da un metodo di Adams-Bashforth a p-1 passi (predictor).

Risultati fondamentali

$\bullet$ Valgono risultati simili a quelli visti per i metodi ad un passo, in particolare se uno schema é consistente e stabile é convergente, e se h é sufficientemente piccolo i metodi impliciti possono essere risolti per sostituzioni successive.

$\bullet$ I metodi multistep di ordine maggiore di 2 non possono essere incondizionatamente assolutamente stabili . La regione di stabilitá assoluta dei metodi impliciti contiene di regola la regione di stabilitá assoluta dei corrispondenti metodi espliciti.

$\bullet$ Se in un metodo Predictor-Corrector si effettua una sola iterazione del corrector, l'ordine di consistenza é lo stesso che si otterrebbe con la soluzione esatta del metodo implicito.