AL310 - Istituzioni di Algebra Superiore:
Teoria delle equazioni

Docenti	Francesco Pappalardi
Ricevimento	Martedì 11 - 13
Ufficio	209
Telefono	06 5733 8247
E-mail	pappa at mat.uniroma3.it
TUTORE	TBA
Lezioni:	Martedì 16 - 18 (Aula M3) Mercoledì 11 - 13 (Aula Lab) Venerdì 14 - 16 (Aula M2)
DESCRIZIONE DEL CORSO

1. [24/09/19] Presentazione del Corso. Formule di Cardano per le equazioni di terzo grado. Prerequisiti: Gruppi finiti (ciclici, abeliani, permutazioni, diedrali, alterni, ...). Definizioni e proprietà fondamentali di campi e spazi vettoriali.
2. [25/09/19] Anelli, sottoanelli, ideali, omomorfismi, quozienti, PID, polinomi, .... Teorema Fondamentale di Omomorfismo per anelli. (pagine 7-10 delle note di Milne)
3. [27/09/19] ancora sui polinomi. Fattorizzazione di polinomi. (pagine 11-13 delle note di Milne)
4. [01/10/19] algoritmo per fattorizzare polinomi. Estensioni di campi, esempi, grado di un estensione. Teorema del grado. sottocampi e sottoanelli generati da sottoinsiemi. (pagine 13-16 delle note di Milne)
5. [02/10/19] ancora sui sottoanelli e sottocampi generati da insiemi. Estensioni semplici, composto di campi, costruzione di campi mediante polinomi irriducibili, campi con il gambo. Elementi algebrici e trascendenti, estensioni trascendenti. proprietà dei numeri algebrici e di quelli trascendenti. Morfismo di valutazione. estensioni finite vs estensioni algebriche e finitamente generate. (pagine 14-18 delle note di Milne)
6. [04/10/19] Esercitazione tenuta da Fabrizio Barroero
7. [08/10/19] proprietà del polinomio minimo. elementi algebrici e trascendenti e proprietà. Storia della trascendenza. (pagine 17-20 delle note di Milne)
8. [09/10/19] Proiezione del Video Galois storia di un matematico rivoluzionario. Introduzione a GP-Pari: installazione e primi comandi per lavorare con numeri primi e campi numerici. Dimostrazione della trascendenza di un numero di Liuville (pagina 20 delle note di Milne)
9. [11/10/19] Costruzioni con riga e compasso: definizioni. i numeri reali costribili sono un campo. caratterizzazione algebrica dei punti costruibili. la quadratura del cerchio, la duplicazione dell'angolo e la trisezione dell'angolo. Costruzione dei poligoni regolari (inizio). (pagine 500-506 del capitolo 13 del libro di Artin)
10. [15/10/19] Numeri costruibili: bisezione di un angolo, Impossibilità di soluzione con riga e compasso dei problemi classici. Duplicazione del cubo, trisecazone di un angolo, quadratura del cerchio. Poligoni regolalari costruibili: se un poligono regolare con p lati, p primo, è costruibile allora p è un primo di Fermat. Se un numero reale alpha genera un estensione di Galois di grado un potenza di due allora α e' costruibile. Caratterizzazione dei poligoni regolari che sono costruibili con riga e compasso. Descrizione di tutti i sottocampi dei campi ciclotomici: (Q(ζ_n), n=3,4,5,6,7,8,9,10). Campi algebricamente chiusi (inizio) (pagina 24 delle note di Milne)
11. [16/10/19] Campi algebricamente chiusi (fine). Omomorfismi da estensioni semplici. Campi di spezzamento (inizio). (pagine 24-28 delle note di Milne)
12. [18/10/19] Campi di spezzamento (continua). Proprietà dei campi di spezzamento (pagine 28-30 delle note di Milne)
13. [22/10/19] Campi di spezzamento (fine). Radici multiple, polinomi separabili, esempi di polinomi inseparabili, campi perfetti (inizio) (pagine 30-32 delle note di Milne)
14. [23/10/19] Campi perfetti (fine). Gruppi di Automorfismi di campi (pagine 32-37 delle note di Milne)
15. [29/10/19] Esercitazione Inizio soluzione del secondo Tutorato 18/19
16. [05/11/19] Esercitazione soluzione del secondo Tutorato 18/19. Soluzione Prova in Itinere
17. [06/11/19] Esercitazione Fine soluzione del secondo Tutorato 18/19. Soluzione Prova in Itinere
18. [08/11/19] Esercitazione
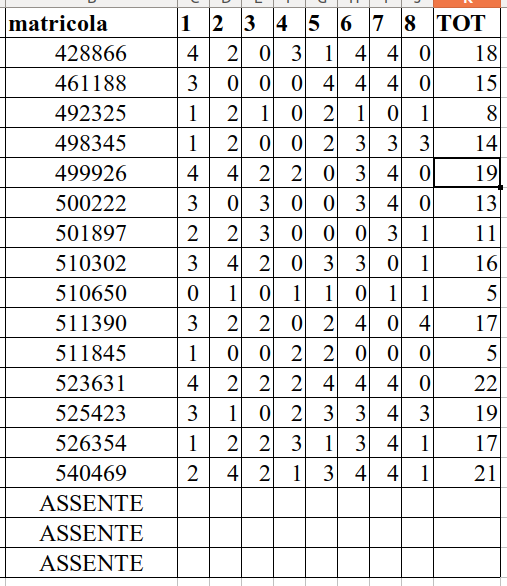
19. [13/11/19] Prima prova in itinere
20. [19/11/19] Esercitazione correzione della prima prova in itinere (inizio)
21. [20/11/19] Esercitazione correzione della prima prova in itinere (fine)
22. [22/11/19] Definizione di estensione di Galois e sue caratterizzazione. Esempi. Enunciato del Teorema Fondamentale della corrispondenza di Galois (pagine 38-40 delle note di Milne)
23. [26/11/19] Dimostrazione del Teorema Fondamentale della corrispondenza di Galois. Esempi, applicazioni. (pagine 41-44 delle note di Milne)
24. [27/11/19] Esempi e applicazioni del Teorema Fondamentale della corrispondenza di Galois. Esempi di reticoli di sottocampi. Numeri costruibili ed estensioni di Galois. Dimostrazione del Teorema di Gauss per poligoni regolari. (pagine 41-44 delle note di Milne)
25. [29/11/19] Esercitazione Dai Tutorati 5 e 6 dell'anno accademico 18/19
26. [03/12/19] Gruppi di Galois come gruppi di permutazioni. Gruppi transitivi e polinomi irriducibili. Gruppi di Galois di permutazioni pari.
27. [04/12/19] Permutazioni pari e sottocampo generato dalla radice quadrata del discriminante. Esempi. Gruppi risolubili e estensioni risolubili. Enunciato del Teorema di Galois sulla risolubilità dei polinomi. La definizione di discriminante. Proprietà del discriminante. Gruppi di Galois di polinomi di grado 2 e 3. Classificazione dei sottogruppi transitivi S₃, S₄ e S₅ (senza dimostrazioni).
28. [06/12/19] Esercitazione esercizi svolti dai tutorati degli anni precedenti.
29. [10/12/19] ancora sul Discriminante di un polinomio. formula per il discriminante in termini della derivata del polinomio. Discriminanti di polinomi di grado 2 e 3. Il discriminante dei p-esimi polinomi ciclotomici.
30. [11/12/19] Gruppi di Galois e radici di polinomi di grado tre. Polinomi di grado quattro. Risolvente cubica. Esempi di polinomi di grado quattro con tutti i possibili gruppi di Galois. Problema inverso di Galois (enunciato). Polinomi aventi gruppo di Galois isomorfo a S_p.
31. [13/12/19] Esercitazione Esempio del reticolo dei sottocampi di un'estensione quaternonica. Esercizi sui polinomi di grado 4.
32. [17/12/19] Campi finiti. Teorema dell'elemento primitivo.
33. [18/12/19] Irriducibilità dell' m-simo polinomio ciclotomico.
34. [20/12/19] Esercitazione
35. [08/01/20] Esercitazione di preparazione alla seconda prova in itinere
36. [10/01/20] Esercitazione di preparazione alla seconda prova in itinere
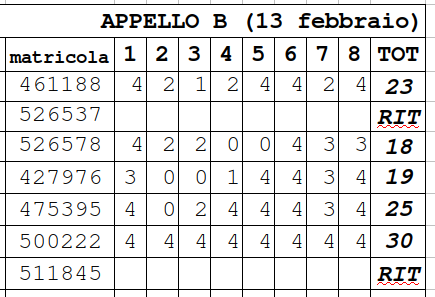
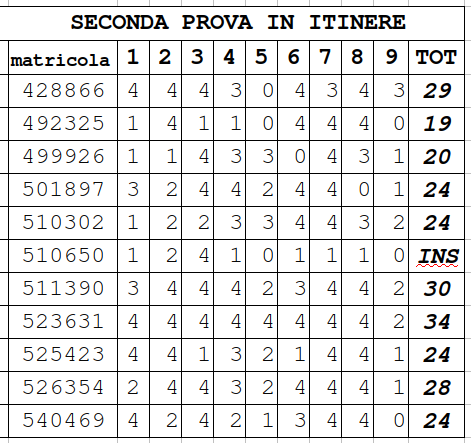
37. [14/01/20] Seconda prova in itinere

1. Appello B 13/02/2020, 11-13, Aula M3
   
2. Appello A 23/01/2020, 11-13, Aula M3
3. Esame di fine semestre 14/01/2020, 11-13
4. Esame di metà semestre 13/11/2019, ore 11-13
   
   
5. Appello C 16/06/2020, 11-13, Aula 211
6. Appello X 25/09/2020, 14-16, Aula 211